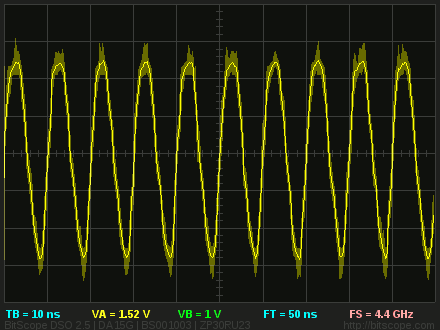
BitScope captures a 100MHz sine wave at 20MSps
The subject of "bandwidth vs sample rate", especially in relation to a PC based digital oscilloscopes like BitScope is one that seems to cause a lot of confusion. To those familiar with the Nyquist-Shannon Sampling Theorem, it seems strange that an analog to digital convertor (ADC) that has a maximum sample rate of 20 or 40 MSps is able to measure signals up to 100 MHz let alone see waveforms that are at even higher frequencies.
However, under the right circumstances it is quite possible to do this and much more.
The key to understanding how this "magic" works is to realize that most signals of interest to an oscilloscope user are periodic. That is, they a have fixed wave shape and they repeat. Indeed it is almost impossible to see any other type of signal with an analog oscilloscope.
A digital oscilloscope like BitScope can of course capture and store any non-periodic waveform, but if we are interested to see waveforms with frequency content higher than half the sample rate, as the specification of many ADCs suggest we can, then it will be limited to periodic waveforms.
ADCs used in BitScopes are designed to exploit this ability by sampling the analog input for a much shorter period of time than a full sample period. That is, they have a very short aperture (ie, time to capture the input signal) but they require additional time to convert the sampled analog value to its encoded digital value.
This short aperture is what enables the ADC to see frequencies much higher than the sample rate alone might suggest, but there is some work to do first to make sense of the data.
If you display a buffer of raw data captured from a signal with higher frequency than half the sample rate, you will still see a waveform; just not the right one! Instead you will see an "alias", or frequency shifted version of the waveform. If certain conditions are met, the alias is unique, meaning you can "unwrap" the raw data to reveal the true waveform.
This process is known as sub-sampling or equivalent-time sampling and is a technique used by many digital oscilloscopes to display high frequency signals. It is similar to a radio circuit where two frequencies are "mixed" to produce the "sum and difference" to shift from high frequency to a lower one. Indeed, ADCs like those used in BitScope are often used to perform this very function in systems like cell phones and WiFi networks.
So, when you read a specification that says "Oscilloscope X has a 100 MHz bandwidth but a 20 MHz sample rate" you'll know it means that using sub-sampling, the scope can display a periodic waveform with frequency components up to 100 MHz. In the case of BitScope, it has a bandwidth of 100 MHz and a sample rate of up to 40 MHz.
Sub-Sampling does not free you from the contraints of the sampling theorem: the bandwidth of the signal must still be less than half the sample rate to avoid destructive aliasing. However, the signal may appear anywhere in the analog bandwidth of the ADC so long as the bandwidth of the signal remains less than half the sample rate.
For example, if you have a 100 MHz analog capture bandwidth and a up to 40 MSps sample rate you can measure a signal with a fundamental frequency of 65 MHz and bandwidth of 20 MHz (ie you can see any frequencies between 65MHz and 85 MHz) which especially useful if the scope has a build-in spectrum analyzer like BitScope. If the signal is not sufficiently bandlimited, it must be filtered to prevent aliased components in the result.
There is one important exception that frees you from this constraint: if the signal is harmonic (ie, there are no frequency components that are not related to the fundamental frequency) and the sample rate is different to and unrelated to the fundamental, it is possible to unwrap all signal harmonics up to the physical analog bandwidth of the scope.
This is how BitScope, and any other digital scope that can perform equivalent-time sampling, can see waveforms at frequencies much higher than the Nyquist-Shannon Sampling Theorem would otherwise imply.
It must be remembered that the analog circuitry must still have an analog bandwidth sufficient to pass the signal to the ADC. BitScope's analog inputs have a 3dB analog bandwidth of 100 MHz. It is even possible to "see" signals at higher frequencies if you are not concerned that the signal will be somewhat attenuated.
For example, this screen-shot shows a 100 MHz signal captured using a BitScope Mini | BS10.
This waveform was captured using equivalent-time sampling running the ADC at close to 20MSps. That is, it captured an alias of the true waveform which was then phase unwrapped and rescaled to display at a sample rate equivalent to 4.4 GSps real-time on a 10 nS/Div time grid for periodic signals.
Put another way, each period of the waveform shown here was constructed from roughly 44 samples captured at different times during the real-time trace and phase unwrapped to locate them on the display at the correct place. A real-time digital scope, sampling at 1GSps, would use 10 samples per period and plot them sequentially and it would be able to capture the waveform even if it was not periodic. However, with equivalent-time sampling a tiny high bandwidth digital scope like BS10 can provide the same result as higher cost oscilloscopes that have much higher real-time sampling rates when used with periodic signals.